Learning-augmented LQC with Untrusted Predictions
Achieve both consistency and robustness for linear quadratic control
History and Motivation
One consequence of the success of machine learning is that accurate predictions are available for many online decision and control problems. For example, the development of deep learning has enabled generic prediction models in various domains, e.g. weather, demand forecast, and user behaviors. Such predictions are powerful because future information plays a significant role in optimizing the current control decision. The availability of accurate future predictions can potentially lead to order-of-magnitude performance improvement in decision and control problems, where one can simply plug-in the predictions and achieve near optimal performance when compared to the best control actions in hindsight, a.k.a., consistency.
However, an important caveat is that the predictions are helpful only when they are accurate, which is not guaranteed in many scenarios. Since many predictions are obtained from black box AI models like neural networks, there is no uncertainty quantification and it is unclear whether the predictions are accurate. In the case when the predictions are not accurate, the consequences can be catastrophic, leading to unbounded worst-case performance, e.g., an unbounded competitive ratio. The possibility of such worst-case unbounded competitive ratio prevents the use of ML predictions in safety-critical applications that are adverse to potential risks.
Consider a toy example of using a robot to track a trajectory online. The trajectory \((y_0,\ldots,y_{T-1})\) is unknown to the robot at the begining and at each time \(t\), the next target position \(y_t\) is revealed to the robot. A straightforward method is to use the model predictive control (MPC) to derive an action \(u_t\) by solving
\[\min_{u_t,\ldots,u_{T-1}} x^{\top}_{t} Q x_{t} + u_{t}^{\top} R u_{t}\] \[\textrm{subject to } \ x_{t+1} = Ax_{\tau} + Bu_{\tau} + \widehat{w}_{\tau} \ \forall \tau=t,\ldots, T-1\]where each \(\widehat{w}_{t}\) is some untrusted ML prediction of the true adversarial perturbation \(w_t\) that may contain error.
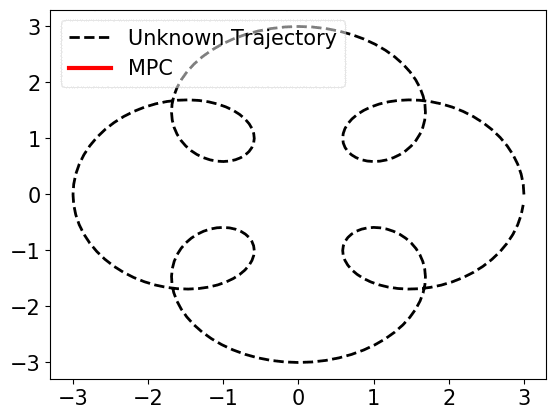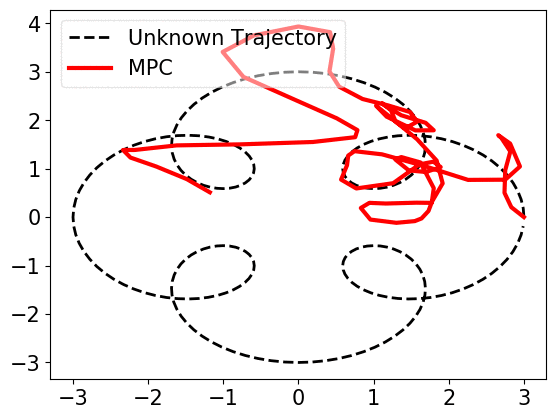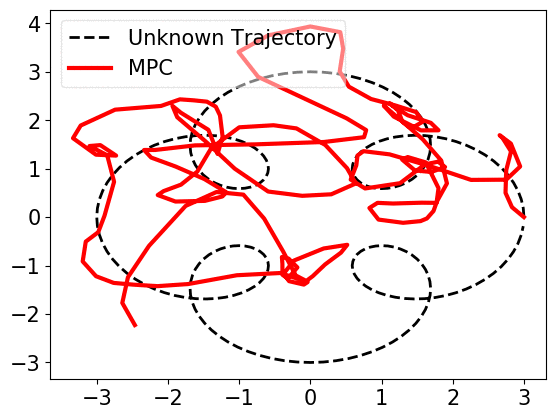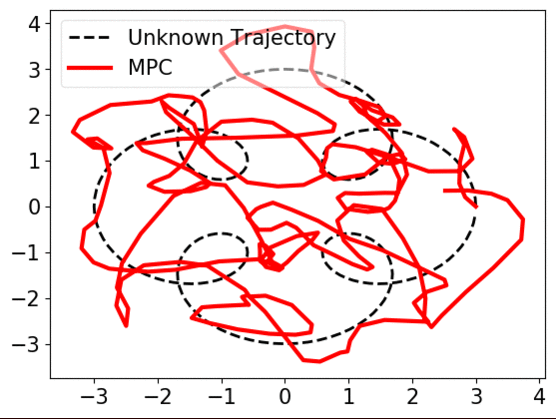
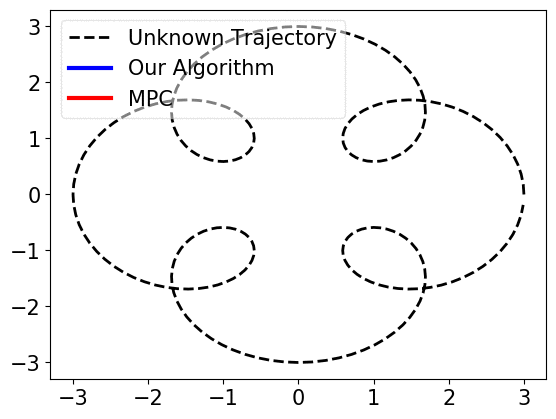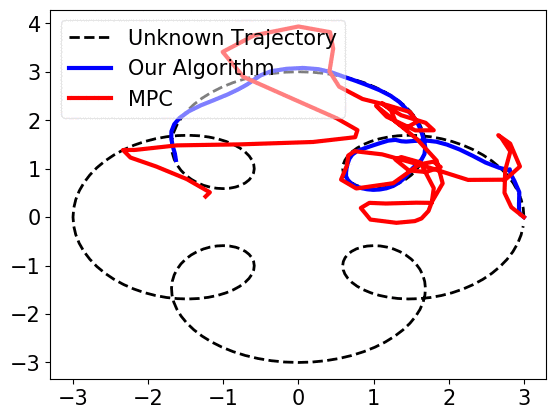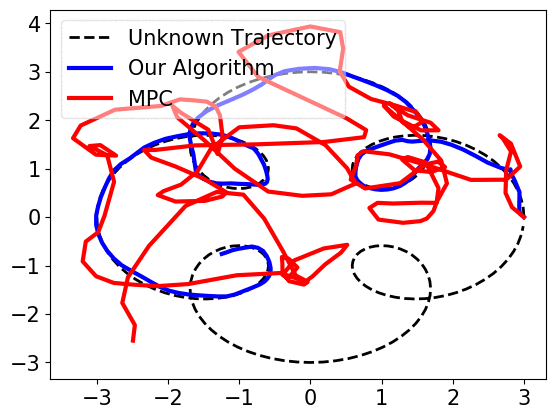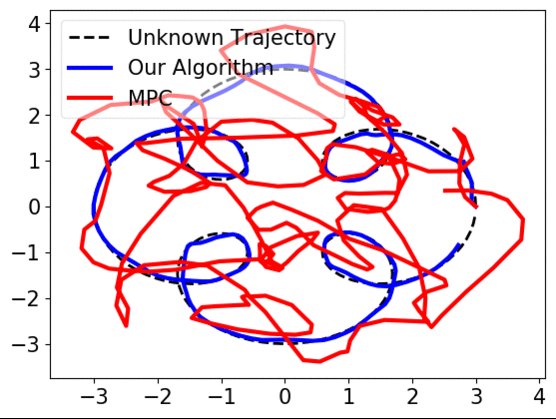
When prediction error, i.e., the mismatch of \(w_t\) and \(\widehat{w}_{t}\) is small, near-optimal actions can be derived. However, if the error becomes large, trusting the predictions, MPC works arbitrarily bad, as shown below.
Main Takeaways
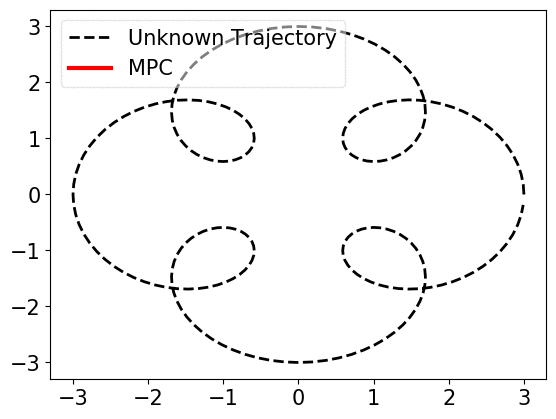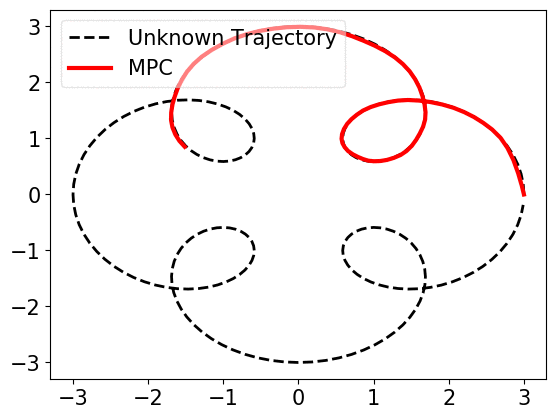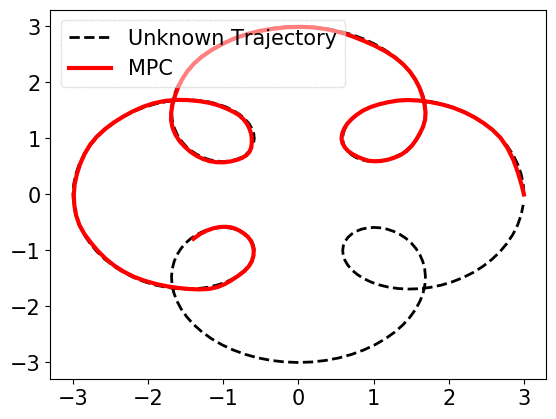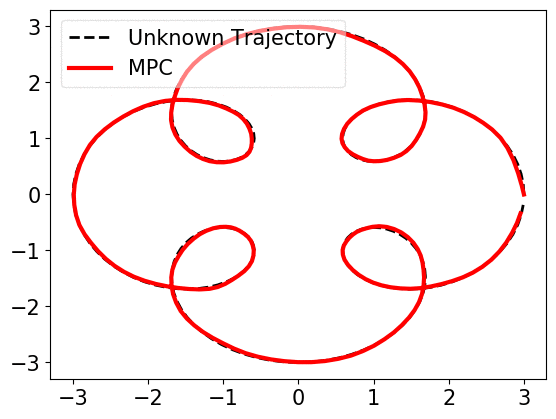
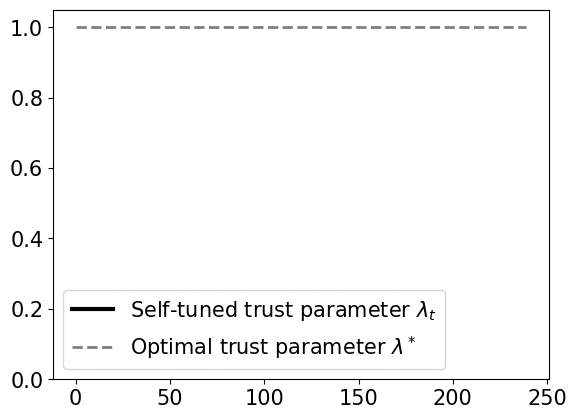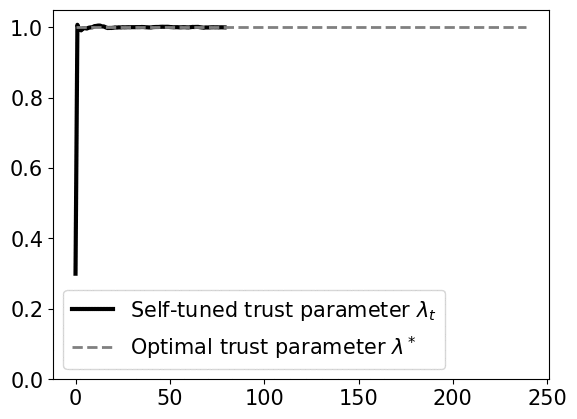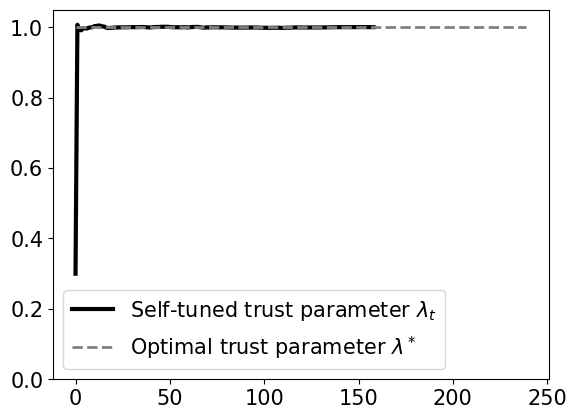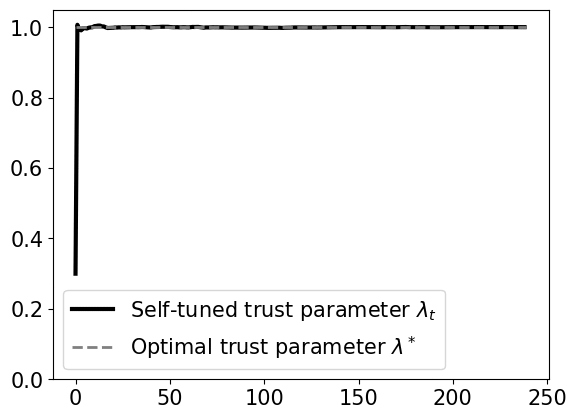
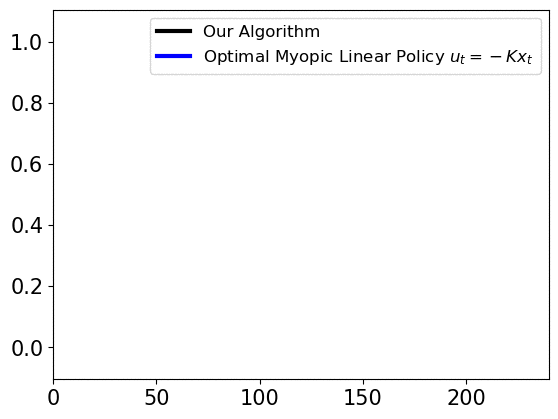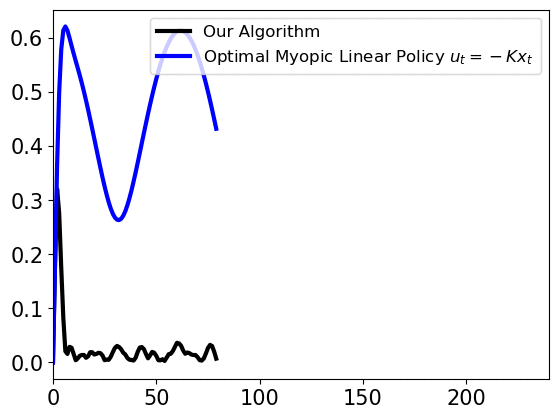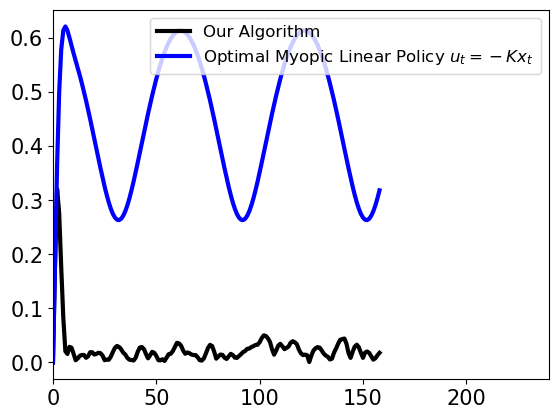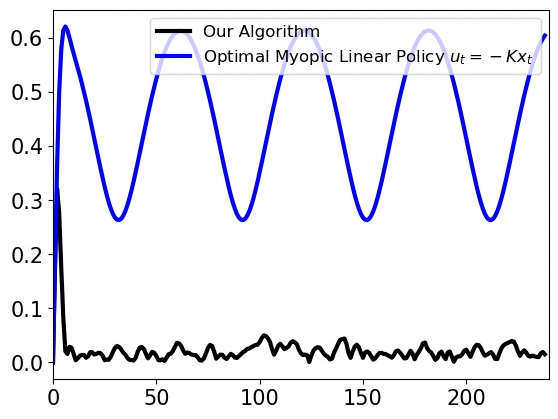
Our work considers an online learning-based control policy that automatically tunes a confidence parameter \(\lambda\) depending on past observations of pertubations and predictions. The parameter weights the policy as a convex combination of a linear policy (that performs well when the prediction error is high) and an MPC policy (that performas well when the prediction error is low):
\[\pi(x) = \lambda \pi_{\mathrm{Linear}}(x) + (1-\lambda)\pi_{\mathrm{MPC}}\]which is equivalent to solving
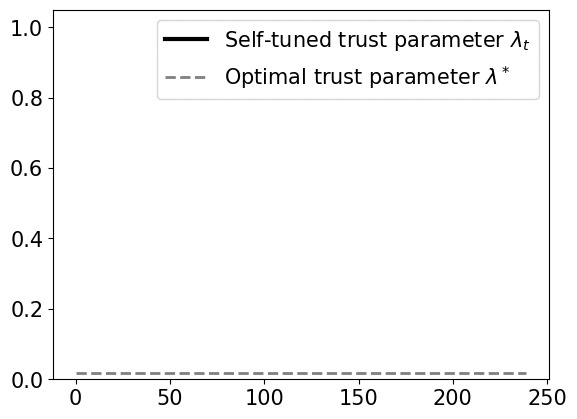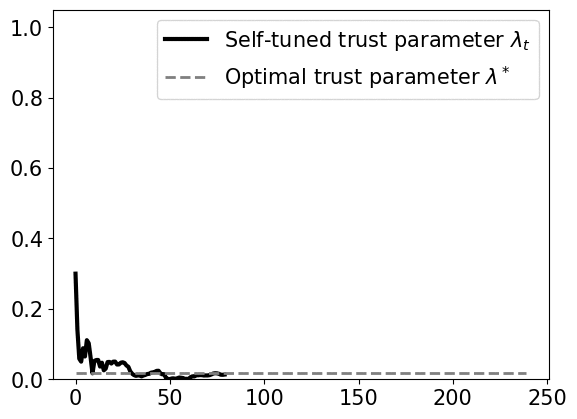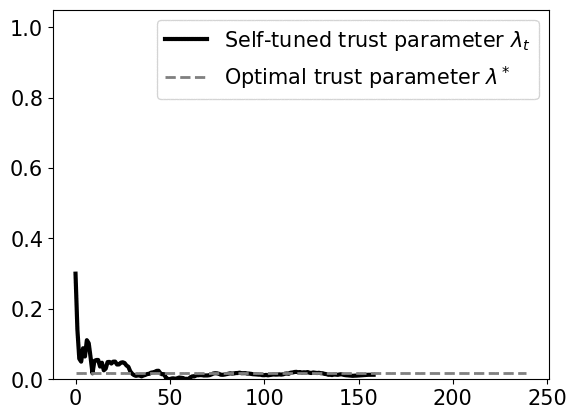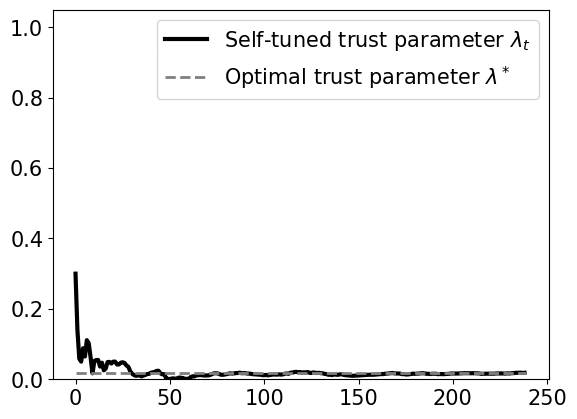
\[\min_{u_t,\ldots,u_{T-1}} x^{\top}_{t} Q x_{t} + u_{t}^{\top} R u_{t}\] \[\textrm{subject to } \ x_{t+1} = Ax_{\tau} + Bu_{\tau} + \lambda\widehat{w}_{\tau} \ \forall \tau=t,\ldots, T-1\]We prove that the self-tuning policy has a bounded competitive ratio, if the variations of perturbations and predictions are small. The policy uses a dynamic confidence parameter \(\lambda_t\) that changes over time. Empirically, the confidence parameter quickly converges to a global optimal confidence level, as shown below.
Reference
[1] Li, Tongxin, Ruixiao Yang, Guannan Qu, Guanya Shi, Chenkai Yu, Adam Wierman, and Steven Low. “Robustness and Consistency in Linear Quadratic Control with Untrusted Predictions.” Proceedings of the ACM on Measurement and Analysis of Computing Systems 6, no. 1 (2022): 1-35.