Tongxin Li | Penalized Predictive Control via Information Aggregation

Problem

This work is the theoretical analysis for a real-world problem considered in this post. We consider the following mathematical model consisting of two controllers – a central controller that knows the objective function of an optimization and a local controller that knows the contraints; neither of the controllers has access to information of the other controller. They can send feedback or information to each other in a closed-loop form. The mathematical framework is shown below.

System model.

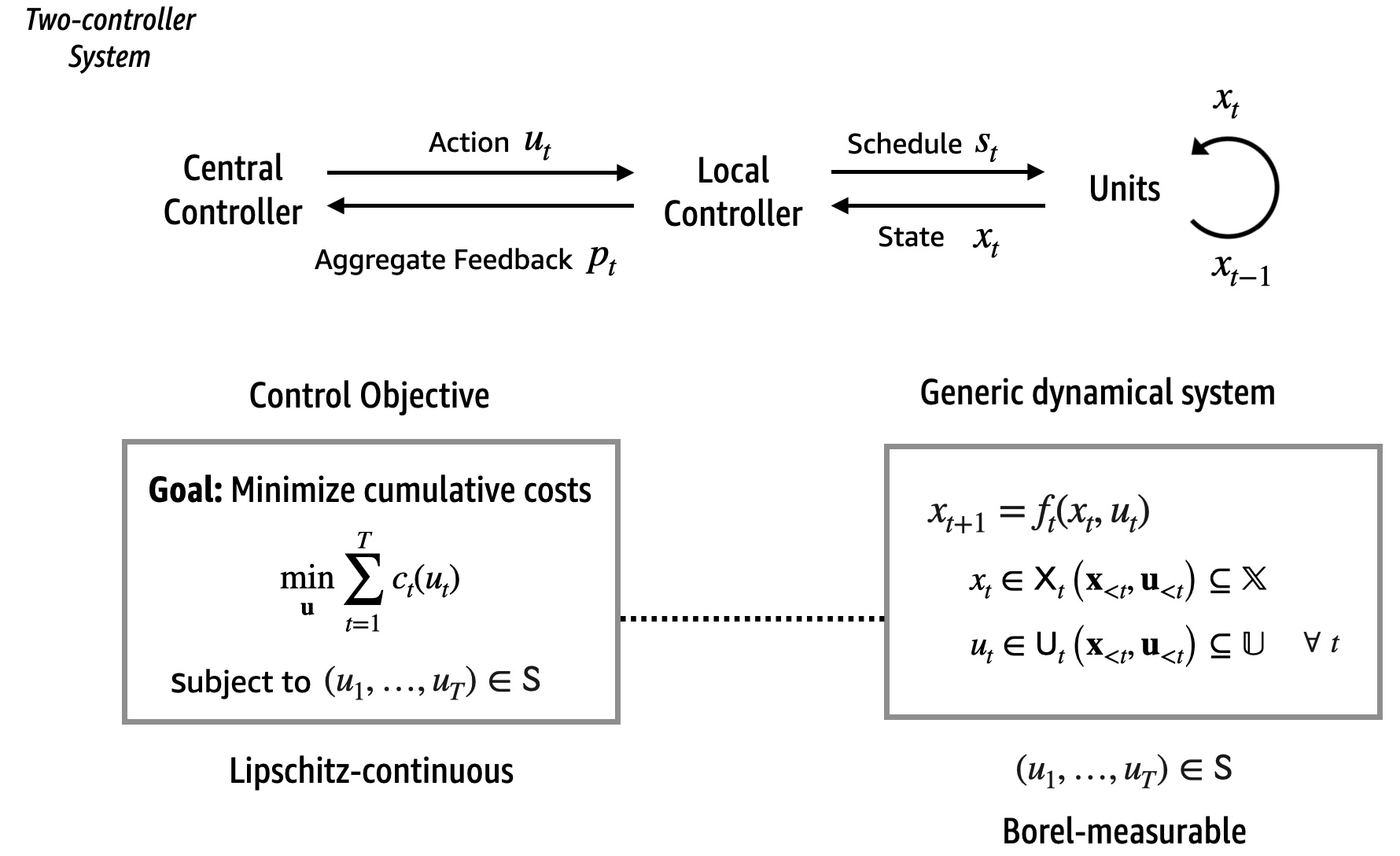
Mathematically, the goal of the two controllers is to jointly solve the following minimization problem online:

\[\min_{u_1,\ldots,u_T}\sum_{t=1}^{T} c_t(u_t)\] \[x_{t+1} = f_t(x_{t},u_{t}), \quad x_{t} \in \mathcal{X}_t(\mathbf{x}_{<t},\mathbf{u}_{<t}), \ u_{t} \in\mathcal{U}_t(\mathbf{x}_{<t}, \mathbf{u}_{<t}), \ \forall t=1,\ldots, T\]

where the deterministic function $f_t$ represents the transition of the state $x_t$, and $u_t$ is the control or action determined by the controller. Crucially, the constraints $\mathcal{X}_t\left(\mathbf{x}_{<t},\mathbf{u}_{<t}\right)$ and $\mathcal{U}_t\left(\mathbf{x}_{<t}, \mathbf{u}_{<t}\right)$ may change over time and they depend on the past history of states $\mathbf{x}_{<t}=(x_{1},\ldots,x_{t-1})$ and actions $\mathbf{u}_{<t}=(u_{1},\ldots,u_{t-1})$. At each time $t$, the action $u_t$ chosen by the online controller incurs a cost $c_t(u_t)$ and the goal is to minimize the cumulative costs without violating the dynamical constraints. Each $c_t(\cdot)$ is a Lipschitz continuous cost function. The dynamic $f_t(\cdot,\cdot):\mathcal{X}_{t}\times\mathcal{U}_{t}\rightarrow\mathcal{X}_{t+1}$ is a Borel measurable function for each $t$. The action space $\mathsf{U}$ is closed and bounded.

Results and Discussion

For this general dynamical system with time-coupling and time-varying constraints, it is not supring that the following negativity result holds.

Theorem (Negativity [1])

For any sequence of actions $\mathbf{u}\in\mathsf{S}$ generated by a deterministic online policy that can access the sets $\{\mathcal{U}_t:t=1,\ldots,T\}$ and $\{\mathcal{X}_t:t=1,\ldots,T\}$, for any $w\geq 1$, the dynamic regret is $\mathsf{Regret}(\mathbf{u}) = \Omega\left(d(T-w)\right)$ where $d:=\mathsf{diam}(\mathsf{U}):=\sup\{||u-v||_2:u,v\in \mathsf{U}\}$ is the diameter of the action space $\mathsf{U}$, $w$ is the prediction window size and $T$ is the total number of time slots.

The theorem indicates that without any assumptions on the constraints, it is impossible to achieve a sub-linear dynamic regret.

In our work, we consider a specific encoding of the constraints motivated by information theory. The feasibility information is represented by a vector $p_t$ (if the action space $\mathsf{U}$ is discrete) or a density function (if the action space $\mathsf{U}$ is continuous). See this post for a real-world motivation of necessities of defining this aggregate feedback.

Our algorithm is a MPC-based policy and it only uses information in $p_{t},\ldots,p_{t+w-1}$ where $w$ is some prediction window size, but not the full constraints. This $p_t$ may contain some future feasibility information and it can be learned by training from historical data. In our analysis, we adopt an ideal assumption that this $p_t$ is accurate, whose efficacy can be validated in practice.

\[\mathbf{u}_{t: t+w-1} = \mathrm{arginf}_{\mathbf{u}_{t: t+w-1}} \sum_{\tau=t}^{t+w-1} \left(c_\tau(u_\tau) - \beta\log p_\tau(u_\tau|\mathbf{u}_{< \tau})\right)\] \[\text{subject to } \ \mathbf{u}_{t: t+w-1}\in\mathsf{U}^{t+w-1-t+1}\]

Our algorithm for the two-controller system is presented below where $\pi_{\mathrm{PPC}}$ provides an action $u_t$ at each time $t$ by solving the optimization above and $\psi_{\mathrm{IA}}$ is some learning-based information aggregator that maps a state $x_t$ to aggregations $p_t,\ldots,p_{t+w-1}$.

Penalized predictive control.

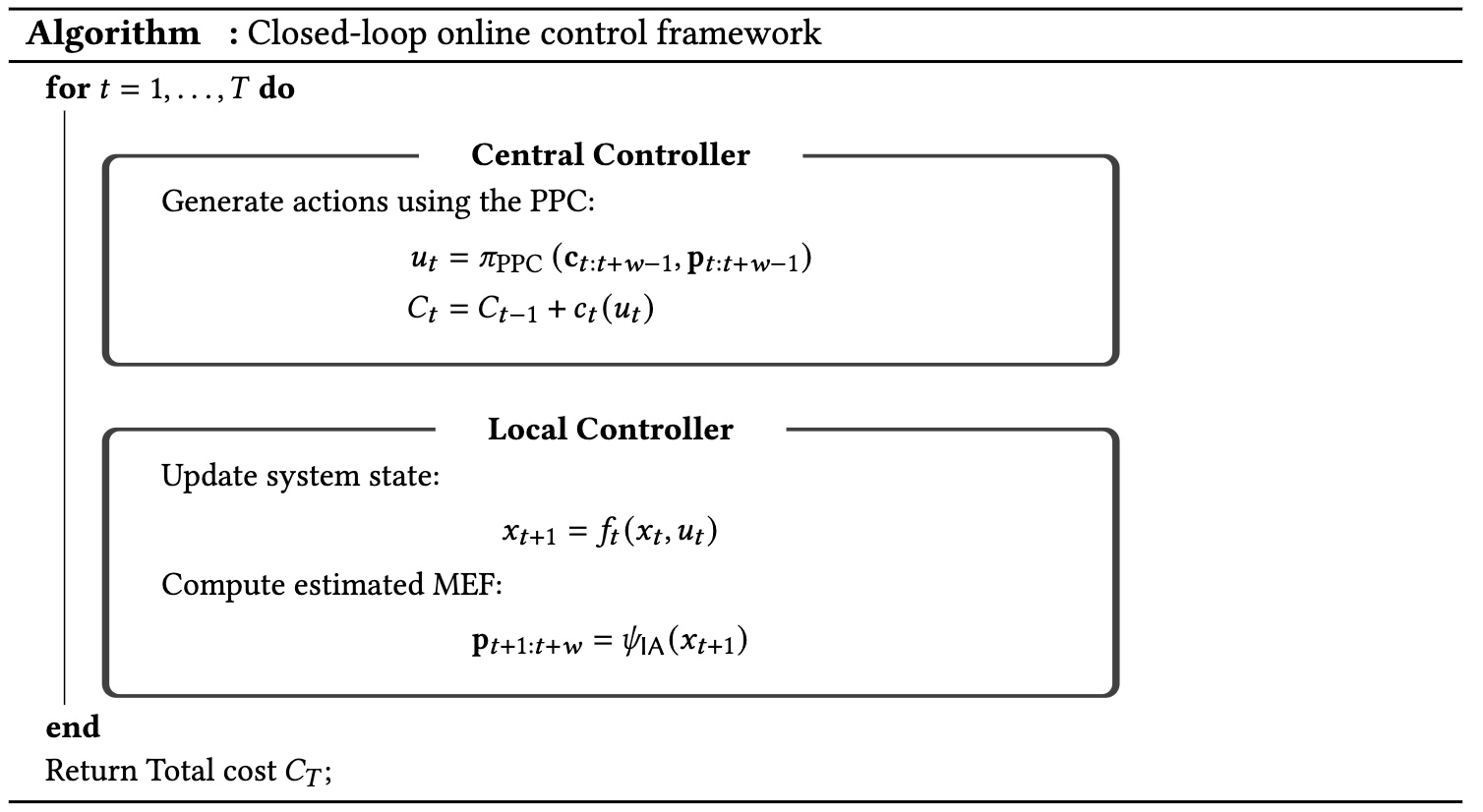
Our results first show that, under certain conditions on the constraints, it is possible to achieve a sub-linear dynamic regret, if $w=\omega(1)$. In detail, we show that

Theorem (Regret Bound [1])

Under some causal invariance assumptions on the constraints, the dynamic regret for the sequence of actions $\mathbf{u}$ given by PPC is bounded from above by

\[\mathsf{Regret}(\mathbf{u}) = O\left( dT\left(\frac{\delta\log\lambda}{\sqrt{w} }+{\frac{\sqrt{\delta}}{w^{1/4}}}\right)\right)\]

where $d$ denotes the diameter of the action space $\mathsf{U}$, $w$ is the prediction window size and $T$ is the total number of time slots.

It can be proven that many types of constraints satisfy the conditions required for the above theorem to hold, including inventory and tracking constraints, e.g.,

$\sum_{t=1}^{T}\|u_t\|^2_{2}\leq \gamma$ where $u_t\in\mathbb{R}^m$ and $\sum_{t=1}^{T} \lvert u_t-y_t\rvert^{p} \leq \sigma$ with $p\geq 2$ and $u_t\in\mathbb{R}$

More details can be found in the paper below.

Reference

[1] Li, Tongxin, Yue Chen, Bo Sun, Adam Wierman, and Steven Low. “Information aggregation for constrained online control.” In Abstract Proceedings of the 2021 ACM SIGMETRICS/International Conference on Measurement and Modeling of Computer Systems, pp. 7-8. 2021.